ALL MATERIAL COPYRIGHT KEVIN SCOTT 2011. LINKS TO THIS SITE ARE WELCOME BUT DO NOT COPY MATERIAL FROM THIS SITE TO ANY OTHER WEBPAGE.
If you find this site useful, please support it by making a donation of $1 to help maintain and develop it. Click on the PAYPAL DONATE button to do this safely. But there is no obligation - please avail yourself of the information and facilities of the site at no charge.
In order that atmospheric pressures measured at different locations with different heights above sea level be comparable for meteorological purposes, they are commonly reduced to values corresponding to a single height datum. This datum is normally the mean sea level. For all locations situated above sea level, this sea level value is theoretical: it refers to the atmosperic pressure which would be exerted if that location was at sea level, i.e at a subterranean depth in practice. Despite this, the use of mean sea level pressure is a very useful standardisation.
There are internationally agreed methods of carrying out this standardisation. The World Meteorological Organisation publishes its International Meteorological Tables in which is used the method described in WMO Technical Note 91, "Methods in use for the reduction of atmospheric pressure". In the USA, the Smithsonian Meteorological Tables are used. Although there are slight variations between methods used by different countries, they all are based on the same equation and, in practice, yield comparable values.
The fundamental equation which relates the atmospheric pressure to altitude is that due to Laplace.
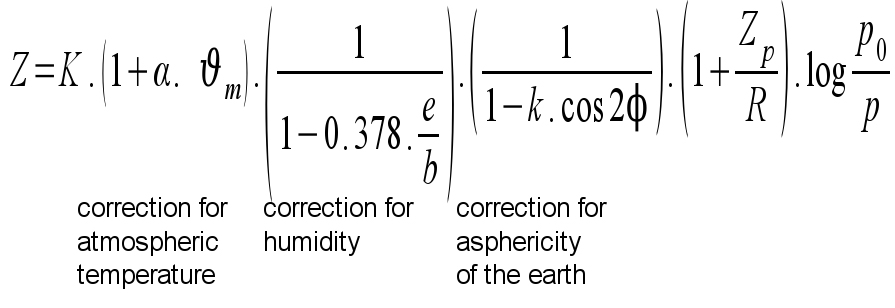
The first term, which is a correction for the temperature of the atmosphere is handled in different ways. In the UK, the average temperature of the air column θm is taken to be the station temperature. In France, θm is calculated assuming a temperature gradient of 0.5 deg C/100 metres. In Italy, 0.6 deg C/100m is used. Other countries use other variants, but in all cases the values are comparable to 0.1 mB.
The second term is a correction for humidity. In the UK it is neglected. In other countries a fixed value is used. In Spain this is a water vapour pressure of 11 mm Mercury. Again these options affect only very slightly the nortmalised pressure.
The third term, the correction for the asphericity of the earth is normally neglected or a fixed value of the lattitude chosen. The fourth term for the variation of gravitational acceleration with height is neglected in the UK and in most other countries.
The table above shows the relative contributions of the factors for which correction is applied. To correct for temperature is evidently important for 1 mB, and correction for humidity important if 0.1mB precision is needed. Other factors are less significant. The author has noted that in high precision barometry, short-term variations or fine structure is observable on the barometric trace, some of which may be due to short term humidity variations. Constructors of sensitive air-barometers in the eighteenth century noted variations of the readings of their instruments when clouds passed overhead.
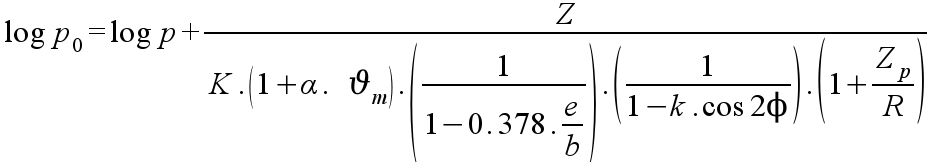
The above equation is a rearrangement of the Laplace Equation for computational purposes. Using the calculator on the left of this page, the reader will be able to verify the magnitudes of the effects of the correcting factors upon the calculated pressure.
A close approximation to the corrections obtained from the Laplace equation is afforded by the formula of Babinet. This gives close correspondence up to 1000 metres and results within 1% to considerably greater heights. The main advantage of it is that it provides a correction for altitude in processors where maths functions are not available or cannot be accommodated.
Babinet's formula can be expressed as:
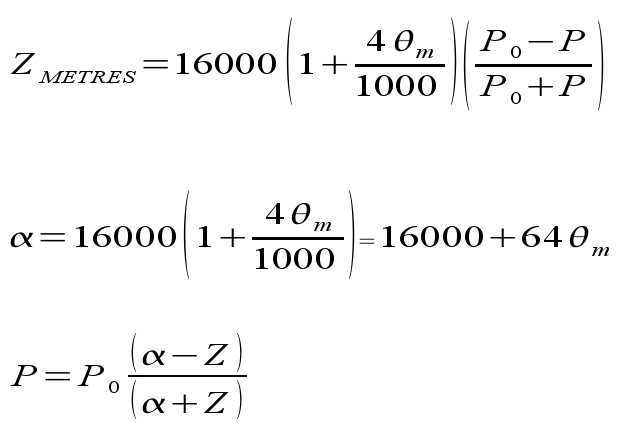The result of using Babinet's formula rather than that of Laplace can be observed by using the calculator.