PRACTICAL TECHNIQUES & KNOW-HOW FOR MAKING & MEASURING IN THE LABORATORY & WORKSHOP

ALL MATERIAL COPYRIGHT KEVIN SCOTT 2011. LINKS TO THIS SITE ARE WELCOME BUT DO NOT COPY MATERIAL FROM THIS SITE TO ANY OTHER WEBPAGE.

If you find this site useful, please support it by making a donation of $1 to help maintain and develop it. Click on the PAYPAL DONATE button to do this safely. But there is no obligation - please avail yourself of the information and facilities of the site at no charge.

A Method for the Absolute Calibration of a Barometer

A traditional mercury barometer can be regarded as an absolute instrument: if the bore is reasonably large, if the glass tube and the mercury are clean, the Torricellian vacuum good and the engraved scales accurate, then the instrument will read the prevailing atmospheric pressure from the point of its construction without reference to any other atmospheric data source. It is thus a primary instrument as opposed to other barometric instruments: electronic, aneroid and sympiesometric.
As these primary mercury-containing instruments give way to non-mercurial, secondary instruments, the need for a method of absolute calibration arises. For many practical purposes, of course, the prevailing atmospheric pressure can be obtained from local weather stations via the Internet or indeed from a mercury barometer in good order if such be available. However, in principle, and in sometimes in practice, the absolute calibration of a secondary instrument becomes desirable. This paper describes such a method which when carefully applied, can result in the absolute calibration of a barometer to 0.1mB precision or better.
The subject of the particular calibration described here was a Texas Instruments Quartz Bourdon Gauge, a secondary instrument with a resolution of about 0.005mB, which was to be used to calibrate Meteormetrics Limited barographs and Sympiesometers. It will be convenient to describe this instrument first, before proceeding to describe the calibration procedure and results.

The Texas Instruments Precision Pressure Gauge

The Instrument to be calibrated is described in two US Patents, Nos 3286529 & 3741015 And the sketches in Figures 1 - 11 have been taken from the Patents. Figure A shows the basic mode of operation of the instrument. A helical quartz bourdon tube, top of which is shown at 11 in Figure 1 carries a small mirror 13 at its lower end which by operation of the motor driven gear train applying torsion to the Bourdon tube can cause the reflected light beam to fall upon the photosensitive sensor plate 27. The whole of the Bourdon tube assembly is maintained at a constant temperature of 40 degrees C by an electronically controlled electric heater. The rotation of the gear train required to achieve this is proportional to the internal gas pressure in the Bourdon tube. In the manual mode, the gear train can be rotated by hand until a null signal is indicated on the meter 30. In the automatic mode, a servo motor operates the gear train continually to maintain the null indication. The turns of the gear train are counted by a 5-digit drum counter readable from the front panel. The instrument appears to have been very well engineered and exhibit extremely small levels of hysteresis and backlash. Figure 2 shows the elevation of the motorised Bourdon system and figure 3, its internal arrangement. Figure 11 shows the front panel of the instrument.

Previous calibration (carried out in December 1991) indicated that the sensitivity to pressure amounted to 182 counts per millibar and that the intercept was zero (i.e. a reading of zero counts for zero pressure). The calibration described here re-measures these quantities and in so doing gives an indication of the stability of the instrument over a 18 year period

Determination of the Slope

Figure 12 shows a simple glass water manometer mounted on a travelling microscope. The two limbs of the manometer were arranged so that the microscope could be focussed on either meniscus without any lateral movement of the microscope being necessary. The precision of the microscope was such that the distance between the two meniscuses could be measured to within 20 microns. The manometer was connected to the pressure gauge via a length of flexible tubing. The gauge was allowed to reach its working temperature before a series of readings were taken from the counter for different water pressures applied via the manometer. At the same time, the prevailing atmospheric pressure was measured with a resolution of 0.1mB, every 3 minutes during the calibration procedure. Measurements were first taken with an ascending pressure and then a descending to detect any hysteresis.

Pressure differences measured with the manometer were corrected for any changes in the atmospheric pressure and expressed in mB. The Atmospheric pressure did change during the course of the calibration procedure by 0.3mB overall. Table I gives the results of this slope calibration.

TABLE 1 - CALIBRATION DATA FOR THE DETERMINATION OF THE SLOPE.


TIME h1 mm h2 mm h2-h1 dP mB Pa mB corrected P COUNTS
10:52:00 46.66 57.87 -11.21 -1.14469519 990.8 -1.04469519 176738
10:55:00 57.42 62.19 -4.77 -0.48708261 990.8 -0.38708261 176866
11:02:00 71.21 67.26 3.95 0.403349331 990.8 0.503349331 177018
11:04:00 82.26 71.28 10.98 1.121209027 990.8 1.221209027 177162
11:07:00 91 74.42 16.58 1.693046053 990.8 1.793046053 177260
11:11:00 102.12 78.15 23.97 2.447666701 990.8 2.547666701 177392
11:14:00 111.02 81.53 29.49 3.011334627 990.8 3.111334627 177493
11:17:00 122.42 85.66 36.76 3.753701624 990.7 3.753701624 177618
11:21:00 131.26 88.95 42.31 4.320432962 990.7 4.320432962 177716
11:25:00 140.85 92.15 48.7 4.972939855 990.7 4.972939855 177833
11:28:00 150.81 96.08 54.73 5.588685796 990.7 5.588685796 177951
11:31:00 161.55 100 61.55 6.285101603 990.7 6.285101603 178081
11:35:00 172.98 103.93 69.05 7.050954764 990.6 6.950954764 178206
11:38:00 184.02 107.63 76.39 7.800469723 990.6 7.700469723 178328
11:42:00 194.34 111.18 83.16 8.491779843 990.6 8.391779843 178439
11:45:00 183.8 107.76 76.04 7.764729909 990.7 7.764729909 178346
11:48:00 175.57 104.77 70.8 7.229653834 990.6 7.129653834 178259
11:52:00 166.12 100.45 65.67 6.705810273 990.6 6.605810273 178153
11:55:00 155 95.61 59.39 6.064535893 990.7 6.064535893 178011
11:58:00 144.69 91.38 53.31 5.443684264 990.7 5.443684264 177901
12:01:00 132.5 85.48 47.02 4.801388747 990.7 4.801388747 177762
12:05:00 122.5 83.08 39.42 4.025324211 990.7 4.025324211 177662
12:08:00 112.32 79 33.32 3.402430307 990.7 3.402430307 177557
12:11:00 100.56 74.36 26.2 2.675380374 990.7 2.675380374 177426
12:15:00 92.4 70.2 22.2 2.266925355 990.8 2.366925355 177339

The counts and corrected pressures from Table 1 are plotted in figure 13.


The least square regression shows a slope of 182.0016 counts per millibar to 4 decimal places. In consideration of the errors of the calibration, this should be expressed as 182.0 +/- 0.1 counts per millibar

Determination of the Intercept

The second stage of the calibration process was carried out using the apparatus of figure 14. A glass flask of approximately 500ml capacity was suspended in a stirred water bath controlled by a temperature controller R. The temperature of the bath could be measured using a type K thermocouple with an ice/water reference F using a Time Electronics Potentiometer with a resolution of 1 microvolt.

Initially, before connecting the flask V to the Pressure Gauge G, the flask and bath were brought to a temperature of about 80 deg C. The connection between V and G was then made with a fine bore tube (0.25mm bore). The apparatus was allowed to equilibrate at a series of temperatures between 25 and 80 deg C, and at each temperature ( carefully measured using the potentiometer) the reading on the gauge was noted. Care was taken to allow sufficient time for the equilibration to take place in each case.

TABLE 2 - CALIBRATION DATA FOR THE DETERMINATION OF THE INTERCEPT.


TIME K ThermEMF mV Temp deg K R076 RDNG PRESSURE CORRECTED READING
0.590277778 2.993 346.2805092 176412 846.1121845 153926
0.597222222 2.796 341.4483149 174302 834.305056 151816
0.600694444 2.859 342.9931814 174976 838.0798293 152490
0.604861111 2.719 339.5607373 173461 829.6928922 150975
0.606944444 2.759 340.5412151 173902 832.0886211 151416
0.613888889 2.547 335.3467387 171658 819.3962818 149172
0.618055556 2.624 337.2328217 172423 824.0047935 149937
0.622916667 2.477 333.6327132 170884 815.2081804 148398
0.625 2.527 334.8569589 171404 818.1995392 148918
0.631944444 2.407 331.9192626 170057 811.0214838 147571
0.633333333 2.456 333.1186173 170483 813.952023 147997
0.636805556 2.331 330.0596045 169203 806.4775394 146717
0.642361111 2.346 330.4265874 169384 807.3742366 146898
0.65 2.248 328.0294574 168314 801.5170171 145828
0.65625 2.308 329.49695 169193 805.1027325 146707
0.664583333 2.162 325.9268195 167601 796.3793685 145115
0.666666667 2.184 326.4646169 167780 797.6934388 145294
0.673611111 2.094 324.2649165 166816 792.3186249 144330
0.684722222 2.008 322.1639275 165862 787.1850054 143376
0.694444444 1.934 320.3568495 165038 782.7695367 142552
0.704861111 1.848 318.2576127 164062 777.6401986 141576
0.716666667 1.77 316.354481 163210 772.9900296 140724
0.729166667 1.704 314.7447591 162446 769.0567868 139960
0.739583333 1.619 312.6724773 161538 763.9933112 139052
0.75 1.546 310.893518 160700 759.6465486 138214
0.750694444 1.54 310.7473337 160640 759.2893577 138154
0.753472222 1.539 310.7229702 160606 759.229827 138120
0.763888889 1.488 309.4806057 160040 756.1941964 137554
0.76875 1.437 308.2385907 159500 753.1594196 137014
0.775 1.396 307.2403623 159040 750.7203186 136554

The data in table 2 was processed and derived as follows:
(a) the EMF values in column 2 were converted to degrees K using the equation:


where v = thermocouple voltage in volts, and an= coefficients as defined in Table 3:

(b)Column 4 of Table 2, shows the reading in counts obtained from the Pressure gauge for each temperature.
(c) To obtain the absolute pressure values in table 2 column 5, the following procedure was adopted:
(i) The reading in column 4 were plotted against the absolute temperature from column 3. This plot is shown in figure 15. Using the slope value obtained from Table 1, the slope of figure 15 was expressed as:

444.708/182.0 = 2.44345 mB/deg K
(ii)This value multiplied by the Absolute temperatures in Column 3, yields the absolute pressures in the volume V for each temperature.
(d) It remains to plot the readings from the pressure gauge, corrected for the intercept in figure 15, against the absolute pressure in column 5.
This plot is shown in figure 16 and is the final calibration plot for the instrument.


Conclusions

The procedure followed produced a useful absolute calibration of a precision instrument for pressure measurement. The key quantity upon which the precision of the whole procedure rests is that of the slope determined in table 1. This has an estimated accuracy of 0.1 in 182, limited by the fact that the travelling microscope only had a 20cm useful travel. Using a longer instrument with a larger range of manometric heights would resulted in a greater precision in the final result.
The use of an enclosed gas volume at a known temperature as an absolute pressure reference worked very well as a calibrating method and the calibration obtained can be relied upon to an accuracy of 0.1mB overall.

 

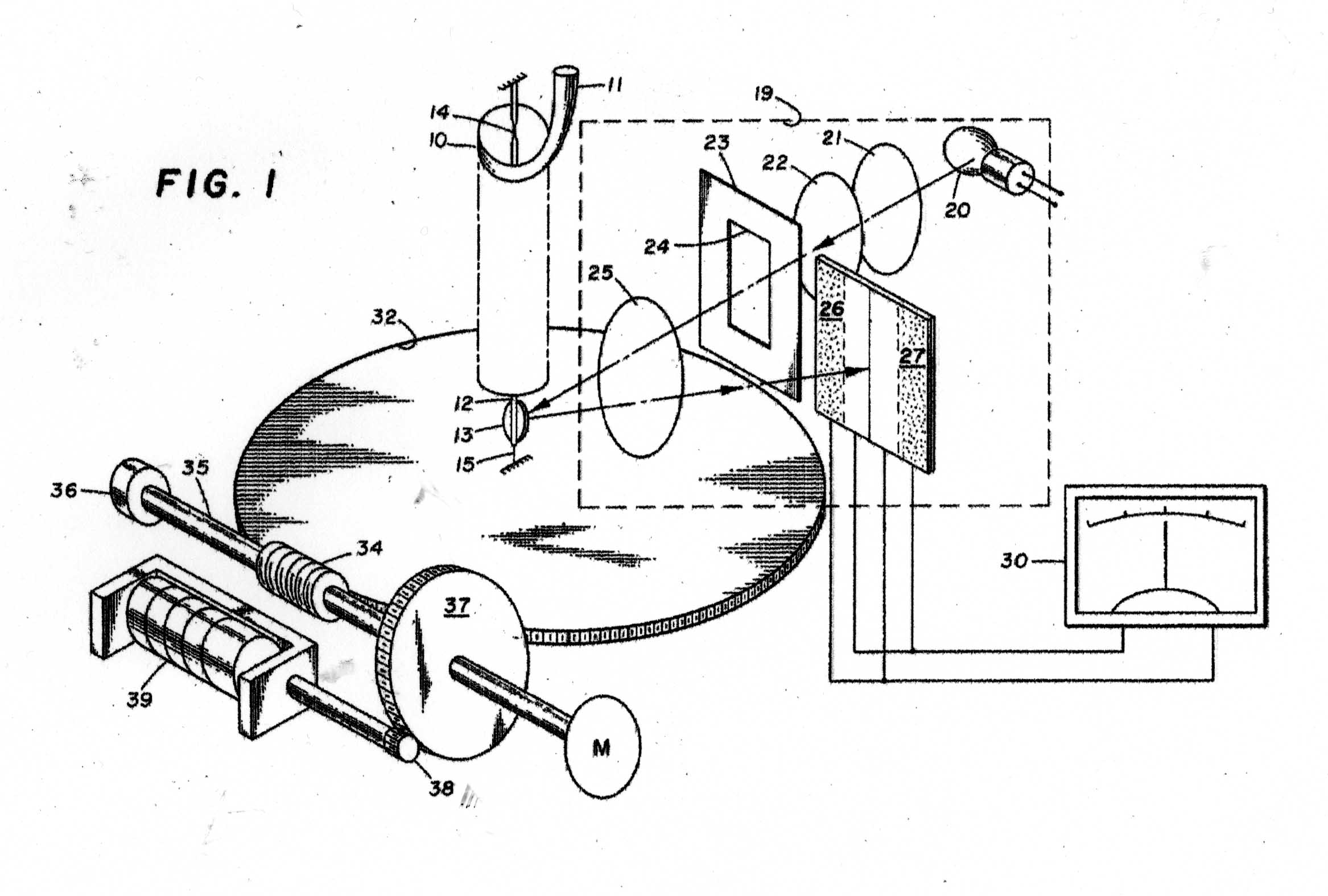
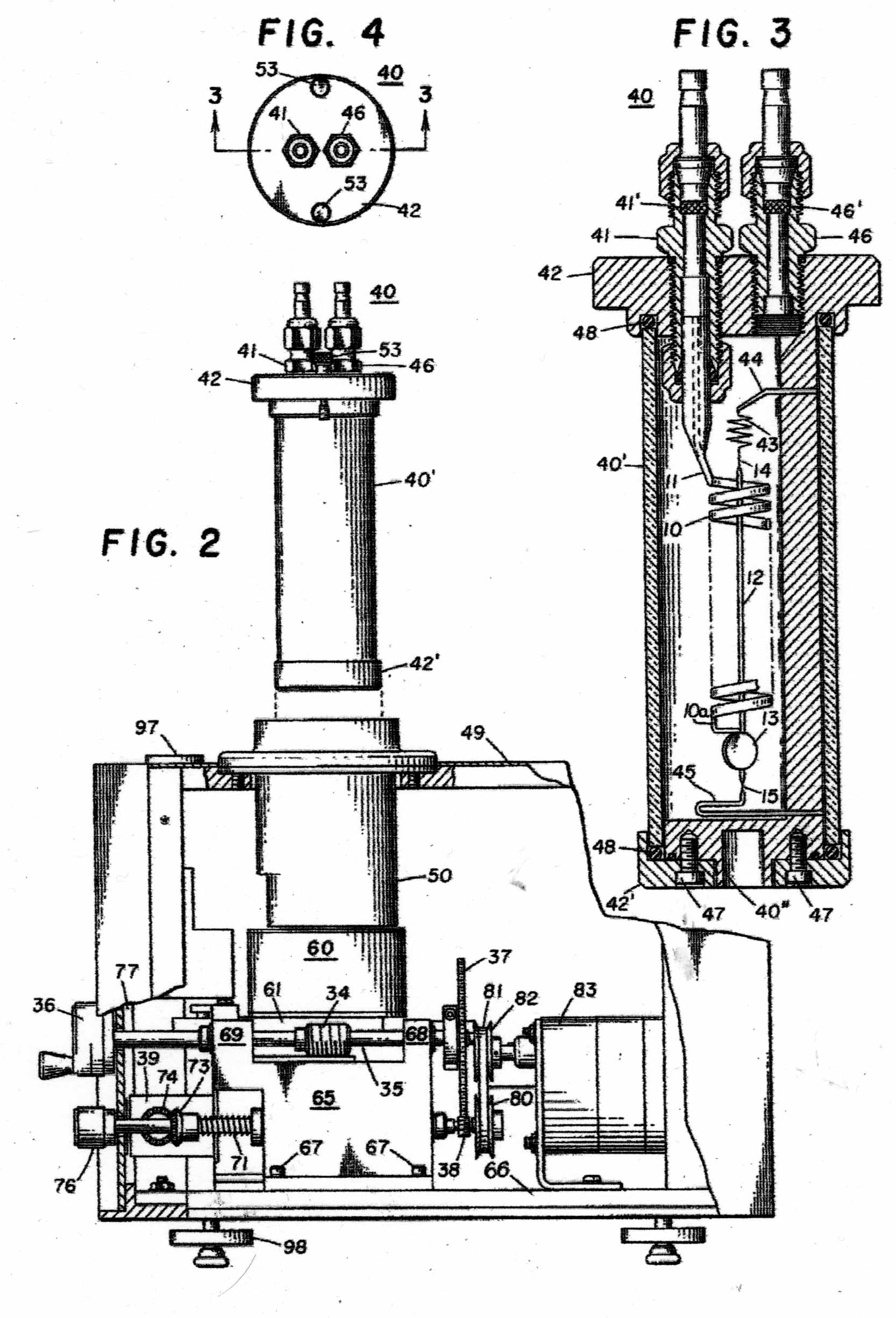
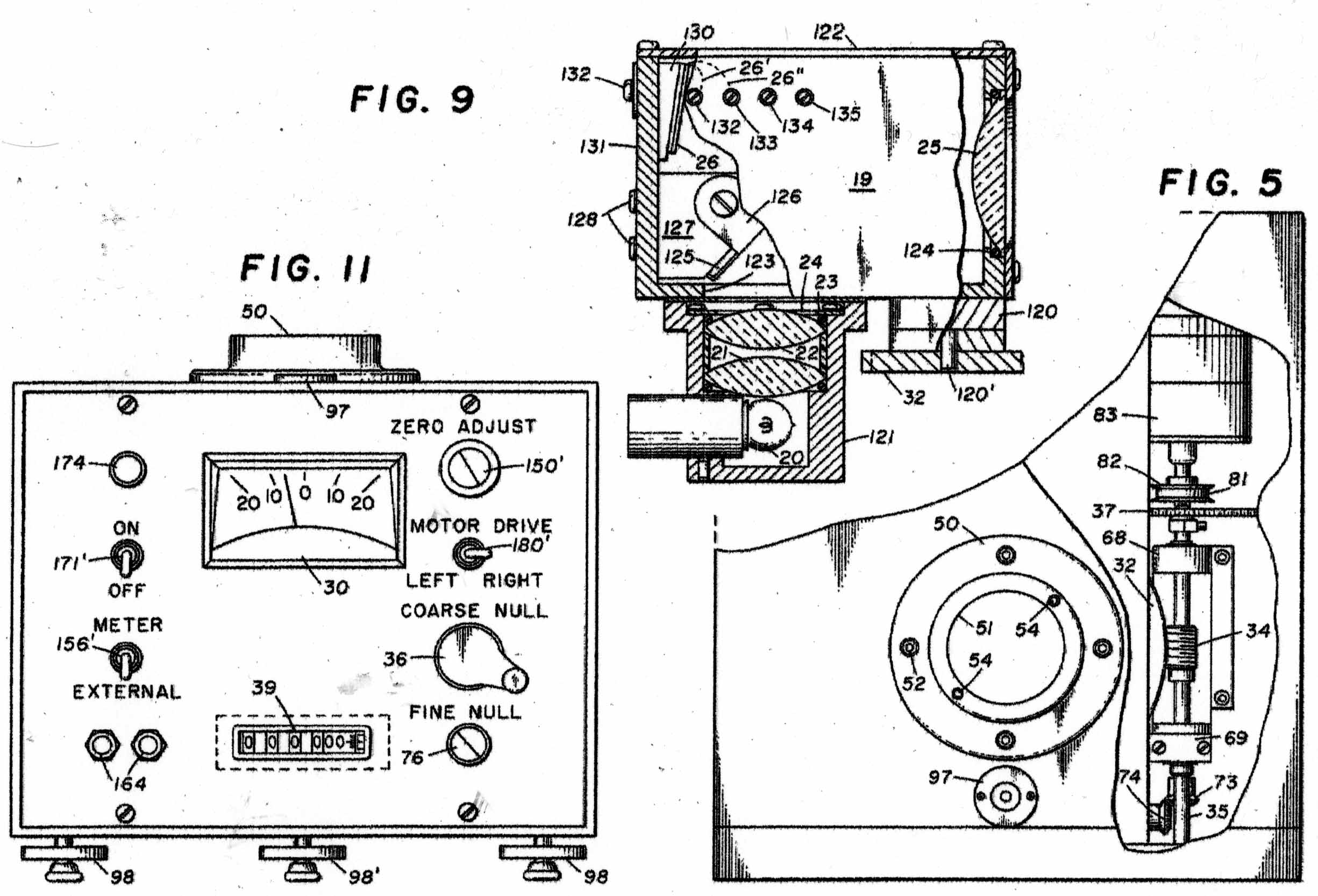
Figure 12, A water manometer mounted on a vertical travelling microscope used for the slope determination.


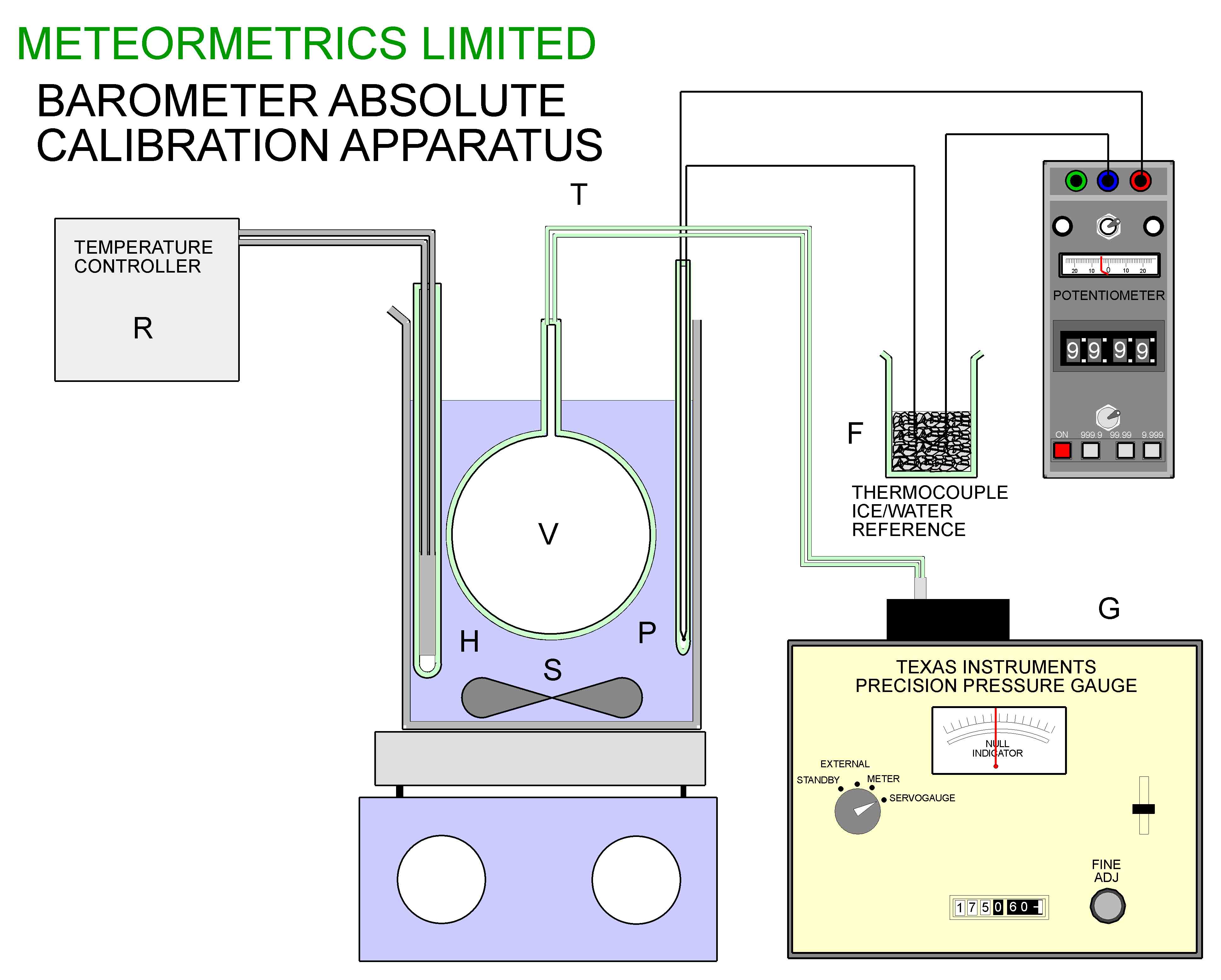
Figure 14, The apparatus for determining the intercept and final calibration


n  an
0 0.2265846
1 24152.1090000
2 67233.4248000
3 2210340.6820000
4 -860963914.9000000
5 48350600000.0000000
6 -1184520000000.0000000
7 13869000000000.0000000
8 -63370800000000.0000000

Table 3, Coefficients of polynomial for K type thermocouples



Figure 15, Plot of pressure gauge reading against absolute temperature


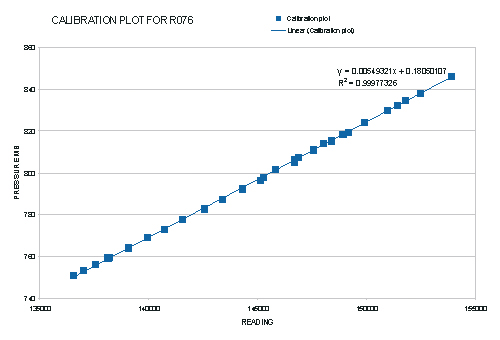
Figure 16, The final absolute calibration plot obtained for the Texas Instruments, Precision Pressure Gauge.